Persamaan kuadrat adalah suatu persamaan polinomial berorde dua. Bentuk umum dari persamaan kuadrat adalah
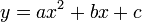
dengan
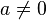
Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari x2, koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.
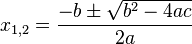
Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa
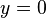 .
.
Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk
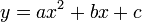
dapat dituliskan menjadi
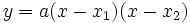 .
.
Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu
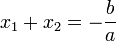
dan
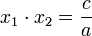 .
.
Ilustrasi dapat dilihat pada gambar.
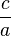 ke ruas kiri
ke ruas kiri
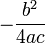 ke ruas kanan
ke ruas kanan
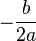 ke ruas kanan
ke ruas kanan
Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini dikriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin:
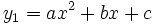 ) dengan suatu garis mendatar (
) dengan suatu garis mendatar ( ). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.
). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.
 dan
dan 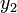 ,
,
diskriminan nol, terdapat hanya satu titik potong antara  dan
dan 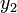 , dan
, dan
diskriminan negatif, tidak terdapat titik potong antara kedua kurva,  dan
dan 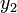 .
.
dengan <img src="http://upload.wikimedia.org/math/0/4/8/048e47341ade7153257cc8dee7ac2c9b.png" alt="x_1 merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila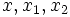 bersifat kompleks, maka yang dimaksud adalah
bersifat kompleks, maka yang dimaksud adalah 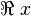 (nilai riil)-nya.
(nilai riil)-nya.
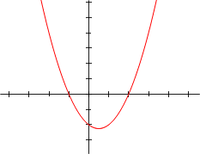 Akar-akar dari persamaan kuadrat
Akar-akar dari persamaan kuadrat
 yang memberikan
yang memberikan
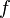 adalah himpunan bilangan riil, maka pembuat nol dari
adalah himpunan bilangan riil, maka pembuat nol dari 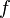 adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.
adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.
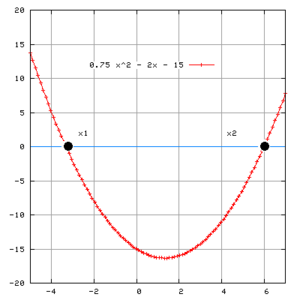
Mengikuti pernyataan di atas, bahwa jika diskriminan berharga positif, kurva persamaan kuadrat akan menyentuh sumbu-x pada dua buah titik (dua buah titik potong), jika berharga nol, akan menyentuh di satu titik dan jika berharga negatif, kurva tidak akan menyentuh sumbu-x.
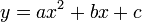
dengan
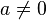
Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari x2, koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
Arti nilai a, b, dan c
- a menentukan seberapa cekung/cembung parabola yang dibentuk oleh fungsi kuadrat. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a < 0 akan menyebabkan parabola terbuka ke bawah.
- b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepatnya adalah -b/2a.
- c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0.
Rumus Kuadratis (Rumus abc)
Rumus kuadratis dikenal pula dengan nama ‘rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk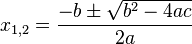
Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa
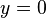 .
.Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk
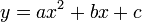
dapat dituliskan menjadi
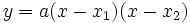 .
.Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu
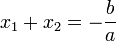
dan
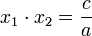 .
.Ilustrasi dapat dilihat pada gambar.
Pembuktian rumus kuadrat
Dari bentuk umum persamaan kuadrat,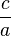 ke ruas kiri
ke ruas kiri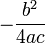 ke ruas kanan
ke ruas kanan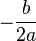 ke ruas kanan
ke ruas kananDiskriminan/determinan
Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar:Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini dikriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin:
- Jika diskriminan bersifat positif, akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional — sebaliknya dapat pula merupakan bilangan irrasional kuadrat.
- Jika diskriminan bernilai nol, terdapat eksak satu akar, dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar ganda, di mana nilainya adalah:
- Jika diskriminan bernilai negatif, tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:
-
-

dan 
-
Akar riil dan kompleks
Persamaan kuadrat dapat memiliki sebuah akar (akar ganda) atau dua buah akar yang berbeda, yang terakhir ini dapat bersifat riil atau kompleks bergantung dari nilai diskriminannya. Akar-akar persamaan kuadrat dapat pula dipandang sebagai titik potongnya dengan sumbu x atau garis y = 0.Titik potong dengan garis y = d
Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadrat (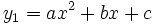 ) dengan suatu garis mendatar (
) dengan suatu garis mendatar ( ). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.
). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol. dan
dan 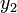 ,
,  dan
dan 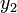 , dan
, dan dan
dan 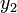 .
.Nilai-nilai y
Akar-akar suatu persamaan kuadrat menentukan rentang x di mana nilai-nilai y berharga positif atau negatif. Harga-harga ini ditentukan pula oleh nilai konstanta kuadrat a:dengan <img src="http://upload.wikimedia.org/math/0/4/8/048e47341ade7153257cc8dee7ac2c9b.png" alt="x_1 merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila
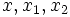 bersifat kompleks, maka yang dimaksud adalah
bersifat kompleks, maka yang dimaksud adalah 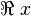 (nilai riil)-nya.
(nilai riil)-nya.Geometri

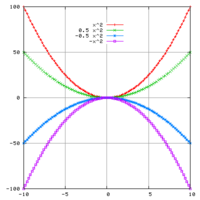
Untuk fungsi kuadrat:
f(x) = x2 − x − 2 = (x + 1)(x − 2), dengan variabel x adalah bilangan riil. koordinat-x dari titik-titik di mana kurva menyentuh sumbu-x, x = −1 dan x = 2, adalah akar-akar dari persamaan kuadrat : x2 − x − 2 = 0.
f(x) = x2 − x − 2 = (x + 1)(x − 2), dengan variabel x adalah bilangan riil. koordinat-x dari titik-titik di mana kurva menyentuh sumbu-x, x = −1 dan x = 2, adalah akar-akar dari persamaan kuadrat : x2 − x − 2 = 0.
 yang memberikan
yang memberikan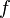 adalah himpunan bilangan riil, maka pembuat nol dari
adalah himpunan bilangan riil, maka pembuat nol dari 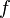 adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.
adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.Mengikuti pernyataan di atas, bahwa jika diskriminan berharga positif, kurva persamaan kuadrat akan menyentuh sumbu-x pada dua buah titik (dua buah titik potong), jika berharga nol, akan menyentuh di satu titik dan jika berharga negatif, kurva tidak akan menyentuh sumbu-x.


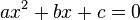
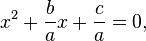



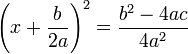


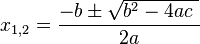



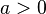 0\!” />
0\!” /> x_2\!” />
x_2\!” />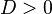 0\!” />
0\!” /> 0\!” />
0\!” />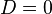

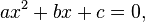

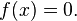
Tidak ada komentar:
Posting Komentar